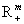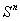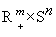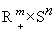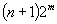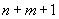| Article ID: | iaor19941040 |
| Country: | Switzerland |
| Volume: | 44 |
| Issue: | 1/4 |
| Start Page Number: | 93 |
| End Page Number: | 113 |
| Publication Date: | Oct 1993 |
| Journal: | Annals of Operations Research |
| Authors: | Yamamoto Yoshitsugu, Yang Zaifu |
In this paper the authors propose a variable dimension simplicial algorithm for solving the variational inequality problem on the cross product of the nonnegative orthant