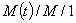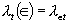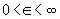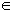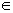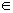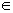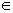| Article ID: | iaor1994362 |
| Country: | United States |
| Volume: | 9 |
| Start Page Number: | 233 |
| End Page Number: | 246 |
| Publication Date: | Feb 1993 |
| Journal: | Stochastic Models |
| Authors: | Chang C., Nelson R. |
| Keywords: | stochastic processes, markov processes |
In this paper, the authors consider a family of