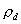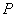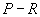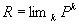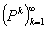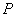| Article ID: | iaor1994264 |
| Country: | Israel |
| Volume: | 29 |
| Issue: | 4 |
| Start Page Number: | 850 |
| End Page Number: | 860 |
| Publication Date: | Dec 1992 |
| Journal: | Journal of Applied Probability |
| Authors: | Pflug G.Ch., Schachermayer W. |
In this paper the authors show that to each distance