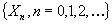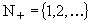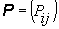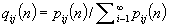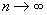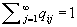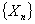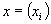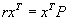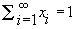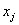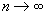Let 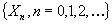 be a transient Markov chain which, when restricted to the state space
be a transient Markov chain which, when restricted to the state space 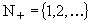 , is governed by an irreducible, aperiodic and strictly substochastic matrix
, is governed by an irreducible, aperiodic and strictly substochastic matrix 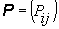 , and let
, and let  . The prime concern of this paper is conditions for the existence of the limits,
. The prime concern of this paper is conditions for the existence of the limits,  say, of
say, of 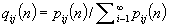 as
as 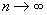 . If
. If 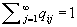 , the distribution
, the distribution  is called the quasi-stationary distribution of
is called the quasi-stationary distribution of 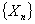 and has considerable practical importance. It will be shown that, under some conditions, if a non-negative non-trivial vector
and has considerable practical importance. It will be shown that, under some conditions, if a non-negative non-trivial vector 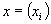 satisfying
satisfying 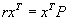 and
and 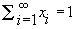 exists, where r is the convergence norm of P, i.e. r=R-1 and
exists, where r is the convergence norm of P, i.e. r=R-1 and  , and T denotes transpose, then it is unique, positive elementwise, and
, and T denotes transpose, then it is unique, positive elementwise, and  necessarily converge to
necessarily converge to 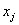 as
as 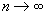 . Unlike existing results in the literature, the present results can be applied even to the R-null and R-transient cases. Finally, an application to a left-continuous random walk whose governing substochastic matrix is R-transient is discussed to demonstrate the usefulness of the results.
. Unlike existing results in the literature, the present results can be applied even to the R-null and R-transient cases. Finally, an application to a left-continuous random walk whose governing substochastic matrix is R-transient is discussed to demonstrate the usefulness of the results.