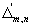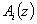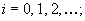| Article ID: | iaor19932366 |
| Country: | United States |
| Volume: | 4 |
| Issue: | 4 |
| Start Page Number: | 333 |
| End Page Number: | 356 |
| Publication Date: | Dec 1991 |
| Journal: | Journal of Applied Mathematics and Stochastic Analysis |
| Authors: | Abolnikov Lev, Dukhovny Alexander |
| Keywords: | queues: theory |
A large class of Markov chains with so-called